This code is to calculate mobility and conductivity of semiconductors by using ab-initio band structure and inputs and it is based on Rode [?, ?, ?] al gorithm. In this code ionized impurity, polar optical phonon scattering due to longitudinal phonon, acoustic deformation scattering, piezoelectric scatter ing, dislocation scattering, alloy scattering, intravalley scattering and neutral impurity scattering are included. Out of these eight scattering mechanism any scattering mechansim can be included or excluded in the simulation.
For the conventional semiconductor devices where the dimensions of the systems are large compared to mean free paths of the carriers, one can use Boltzmann Transport equation (BTE) to describe the transport properties. BTE can be represented as,
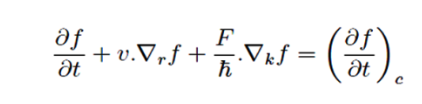
Here f is the single particle distribution function, which is the solution of the BTE. The first term in the above equation represents the explicit time dependence of the distribution function, the second term is a diffusive term and the third one is due to the applied field, F. The term at the R.H.S refers the collision of the carriers by impurities, lattice and other carriers, and these are treated quantum mechanically and that is what makes the approach semi-classical. Once f is obtained all the transport coefficients such as mobility, conductivity, thermo-power etc. can be calculated. The most decisive part of such modeling is how the collision term is treated.
The most common approach is so called relaxation time approximation (RTA), which assumes that the scattering processes would bring back the system to equilibrium after a characteristic time (relaxation time). In most of the ab-initio transport codes, this relaxation time is assumed to be constant.
The RTA is a good approximation, as long as the scattering processes are isotropic and elastic. For such cases, the relaxation time depends only on the scattering processes not the distribution function itself. For processes which are neither elastic nor isotropic, this condition does not hold and therefore one has to treat the collision term numerically. For low field; we can use iterative schemes such as Rode method based on which AMMCR code is developed, while Monte Carlo or path integral method can be used for higher field.
In recent years there have been lots interests in compound semi-conductors particularly III-V semiconductors have higher carrier mobility than Si as they have smaller effective masses. They have direct band gap, therefore they are very suitable for applications such as solar cell and photo-voltaics. However, in these materials there is an important carrier scattering phenomena namely the Polar optical scattering which is neither elastic nor isotropic. This scattering process is very prominent particularly at the temperatures, at which the device would be operational. Therefore, to deal with such carrier scattering mechanisms, one has to use some model of carrier transport other than RTA.
We have implemented the Rode algorithm in the AMMCR code, which is valid for the low electric field.
For low electric field, the total distribution can be written as
fk=f0(k)+xg(k)
Where f0(k) is the equilibrium distribution function and g(k) is the perturbation (non-equilibrium part of the distribution function). The factor x defines the angle between the electric field and the direction of the crystal momentum k.
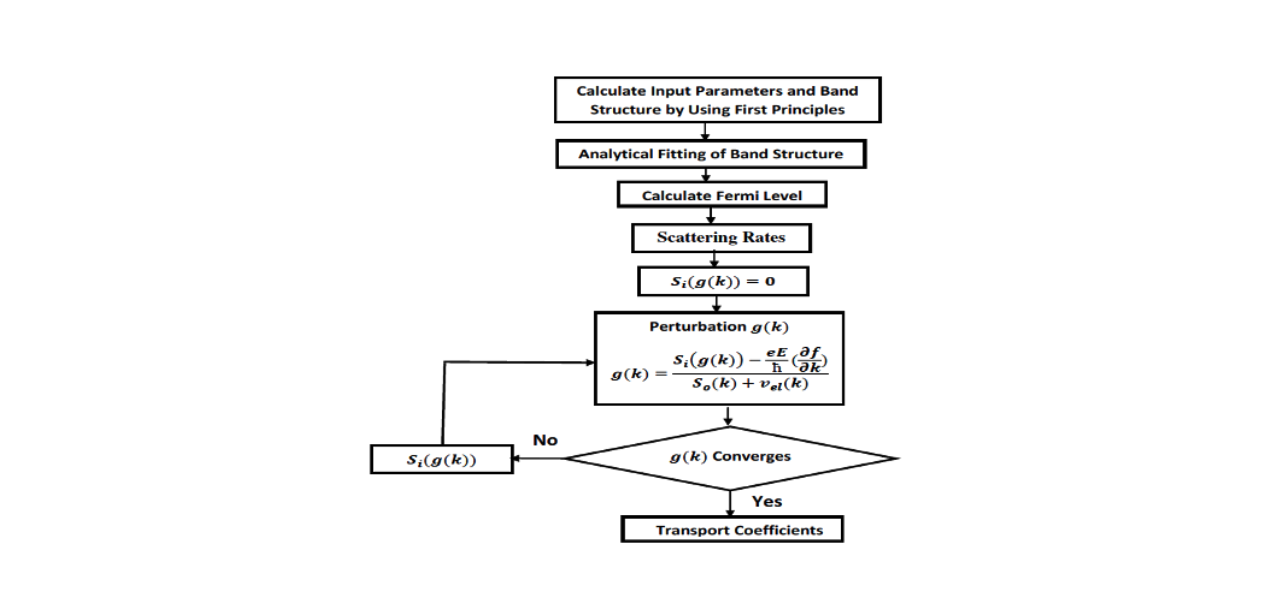
The flow-chart of the code is shown here. First, one has to calculate all the required inputs using the first -principles method. The typical inputs are energy band dispersion curve, density of states, the phonon frequencies and the elastic constants.
We then perform the analytical fitting of the band structure to obtain smooth curves to calculate the group velocity. For a given doping concentration, the Fermi energy is calculated. Then we calculate various scattering rates (discussed below). Finally a loop is used to obtain the non-equilibrium part, g(k) of the distribution function.
The various scattering mechanisms which are implemented in the code are:
Defect induced scatterings from:
Ionized ion impurities
Neutral impurities
Alloy
Dislocations
Scattering mechanisms involving lattice:
Piezoelectric
Intravalley acoustic deformation potential
Polar optical phonons.
Once the loop converges for g(k), all the transport co-efficients are calculated. AMMCR code is written in C++. Currently it is interfaced with Vienna Ab initio Simulation Package (VASP). It is very simple to use. Once compiled, it produces an executable called AMMCR. The executable can be run in a directory where four VASP output files: OUTCAR, EIGENVAL, PROCAR and DOSCAR are present. The specification of the simulation conditions such as temperature, doping concentration, external electric field etc., as well as the materials constants are provided in a file called “input.dat”.
[1] D. L. Rode, Semiconductors and Semimetals (Academic Press, New York, 1975), Chapter 1.
[2] D. L. Rode, Phys. Rev. B 2, 1012(1970).
[3] D. L. Rode, Phys. Rev. B 2, 4036(1970).
[4] G. Kresse and J. Hafner, Physical Review B 49, 14251 (1994).
[5] G. Kresse and J. Furthmller, Physical Review B 54, 11169 (1996).
[6] G. Kresse and J. Furthmullerb, Computational Materials Science 6, 15 (1996).
[7] A. K. Mandia, B. Muralidharan, J.-H. Choi, S.-C. Lee, and S. Bhattacharjee, arXiv:1907.08005 (2019).
[8] A. K. Mandia, R. Patnaik, B. Muralidharan, S. Bhattacharjee and S.C. Lee, Journal of Physics: Condensed Matter 31, 345901 (2019).
[9] A. K. Mandia, R. Patnaik, B. Muralidharan, S.-C. Lee and S. Bhattacharjee, CPC 259, 107697 (2021).